OR-VT-Pharmacy
Publication DOI: 10.1186/s12913-025-13653-1
GitHub Repository: HEGSRR/OR-VT-Pharmacy
Study Reports
- Original study report (generated with the
01_Pharmacy_Accessibility.ipynbnotebook) - Pre-registered analysis plan
- Supplementary materials report
Alternative study versions
Several alternative reports are available for alternative study versions using different study parameters. These are available below for comparison to the original study and check on sensitivity and robustness.
These reports were generated with the 02_Study_Variations.ipynb Jupyter notebook.
Additionally, any two sets of study results can be compared with the 03_Compare_Results.ipynb Jupyter notebook, and selected comparison links are included below.
- Original study parameters
- June 2025 updated data and comparison to 2023
- Technicians as 0.7
- Technicians as 0.3
- Elderly Population
- Mean distance weight
- Additional distance bands
- Census blocks
- Additional distance bands and census blocks and comparison to original study parameters
- Simulated staffing data
The results linked above are discussed in the supplementary materials of the manuscript.
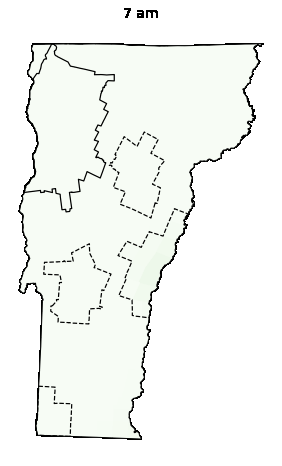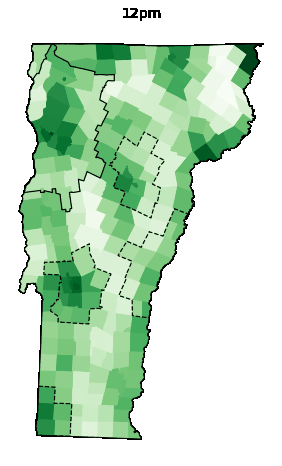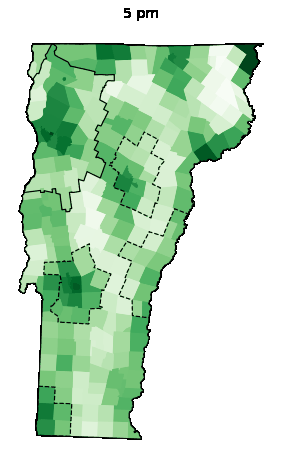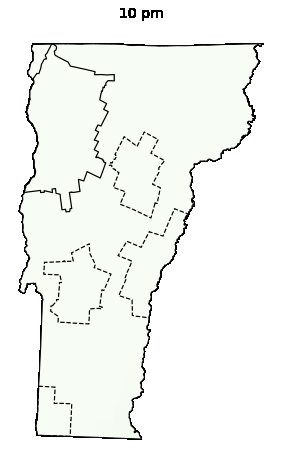
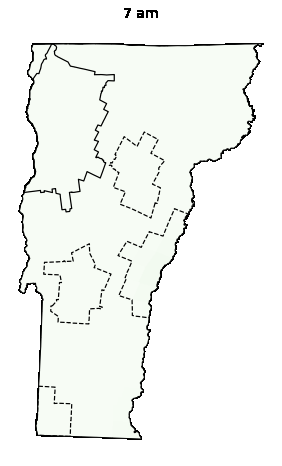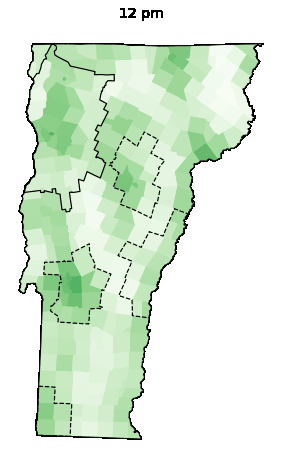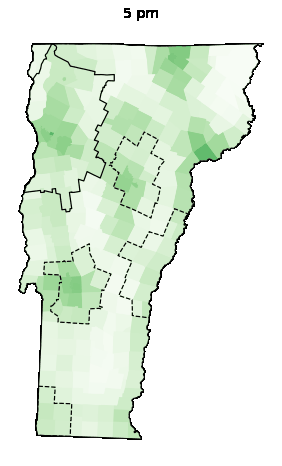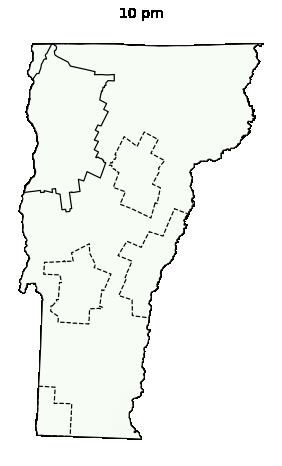
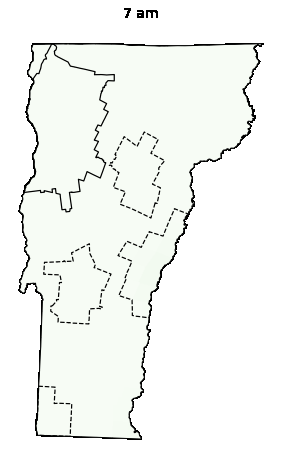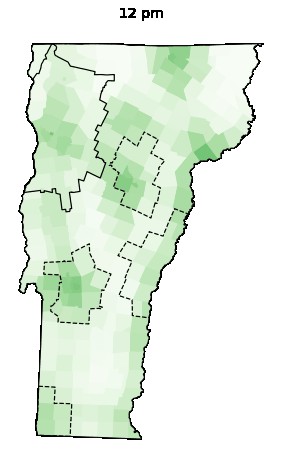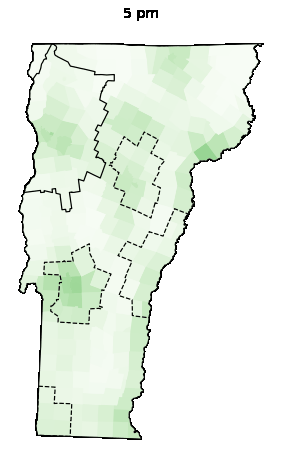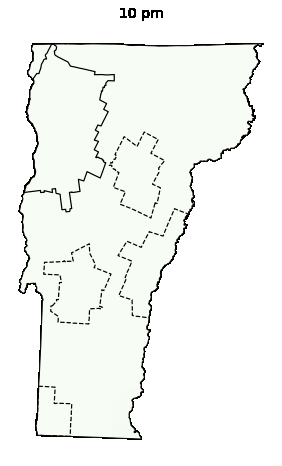
Animations
| Weekday | Saturday | Sunday |
|---|---|---|
 |
 |
 |